
根号を含む式の計算です 写真のマークしてるところなのですが Clearnote
のような2重根号の中には,さらに簡単な形に計算を進められるものがあります。具体的には, と,計算することができます。 ≪計算の手順≫ ① の形に変形する。(内側の の係数を「2」にする) ② 足して ,掛けて となる正の数a,bを見つける。 ③ 式ルートの掛け算・割り算をおこなう場合は、足し算・割り算とは違い、ルート内の数が異なっていても計算できます。 計算方法はルートの外同士・中同士で掛け算・割り算をおこないます。 ルート外の数値がない場合は1として計算します。 計算によって
根号の計算 かけ算
根号の計算 かけ算-これの式も二重根号をはずすための2がついていません。 だから、ちょっと式変形をしていく必要があるのですが 困ったことに、\(\sqrt{15}\)を整理しても2を作り出すのが難しそうです こういう場合にはどうすればいいかというと 強引に2を作り出します!根号を含む分数が幾つもある場合,通分よりも分母の有理化の方が有利 類題 を計算せよ. 解説 やり直す (原式) 引用元の問題は記述式の問題ですが,以下の問題ではWeb画面上での操作性をよくするため,選択問題に変えています. まぐれ当たり
数学 根号を含む計算 平方根など 数学
平方根・累乗根 素晴らしい! の一言です👏 電卓ではできないのでここにたどり着きました。 スマホのパスコード用に桁数が多い数字列を得るため。 スマホを開くのがめんどくさくなったので時間を有効に使えるようになりました。 A=430Hzとした場合英語の root に相当)の頭文字の r を変形したものであるといわもくじ 1 根号(ルート)の足し算・引き算のやり方 11 ルート内の数字が同じだと足し算・引き算できる;
中3数学根号を含む式のいろいろな計算のやり方を解説します! 中学生の勉強方法 115 中2数学文字を含んだ図形の体積の求め方とは?単項式の計算を解説! 中学生の勉強方法 中2数学単項式と多項式の違い、次数について解説し2 分配法則を使う平方根の掛け算・割り算 21 乗法公式を使って式の展開をすると,計算することができます。 ≪計算の手順≫ ただし,すべての2重根号がはずせるわけではなく,「足して ,掛けて となる」正の数a,bが見つからないこともあります。 例 注意 ということを覚えておいて,あらかじめ,a>b>0となるようa
根号の計算 かけ算のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 Tossランド 根号を含む式の加減 |  Tossランド 根号を含む式の加減 | 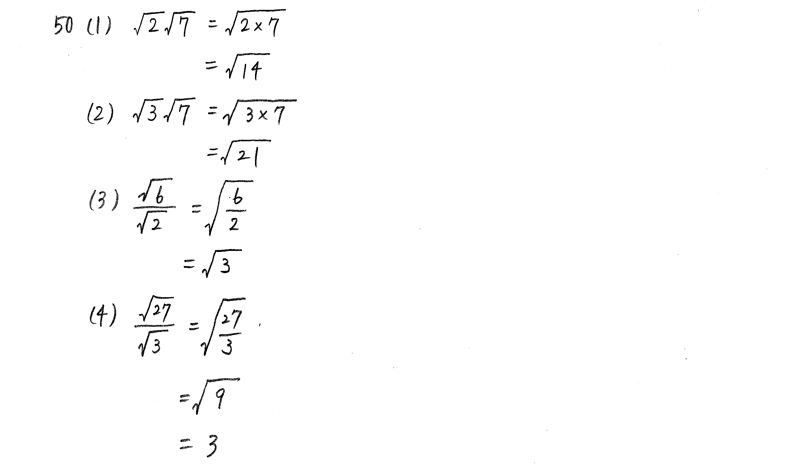 Tossランド 根号を含む式の加減 |
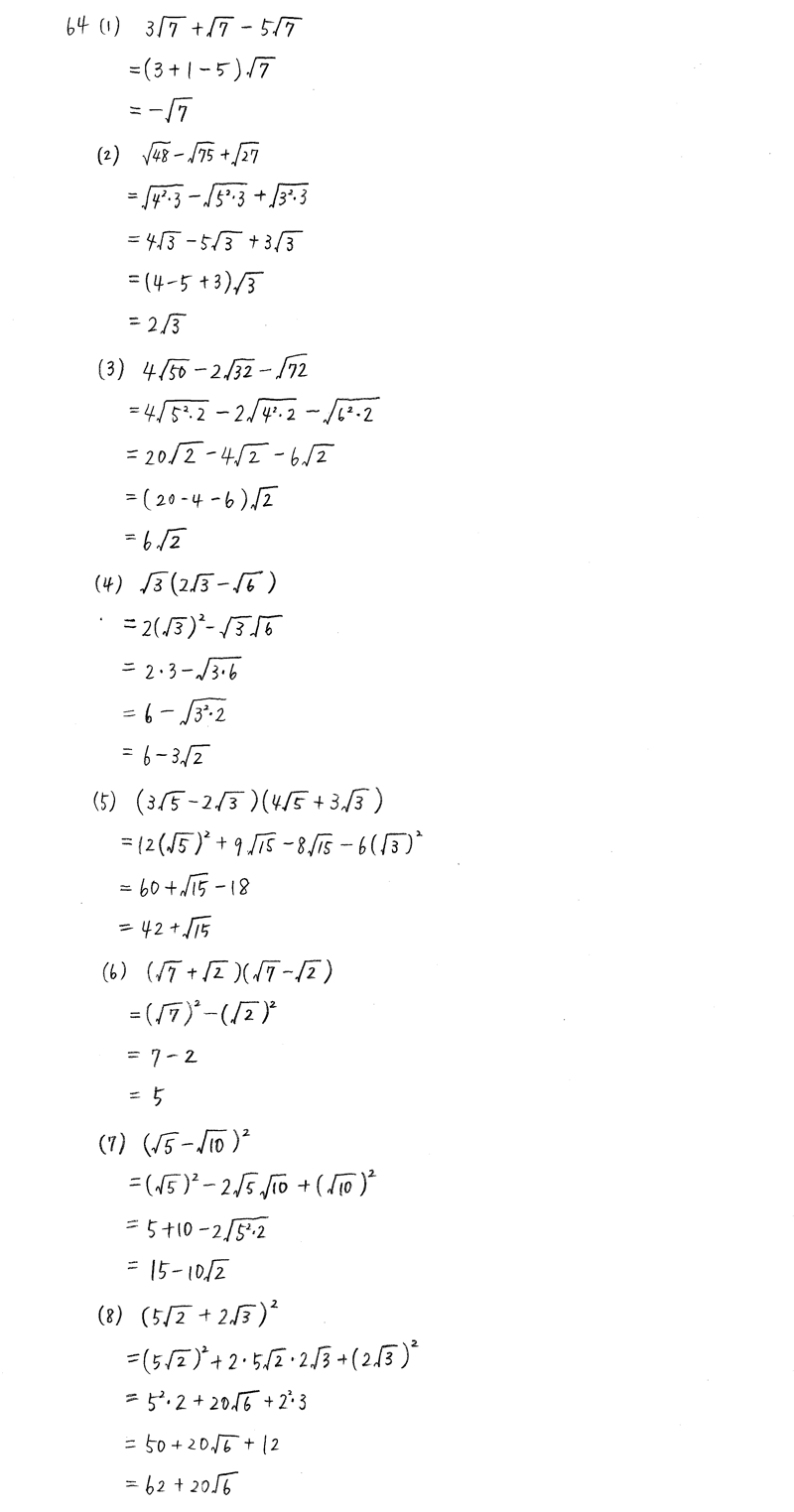 Tossランド 根号を含む式の加減 | 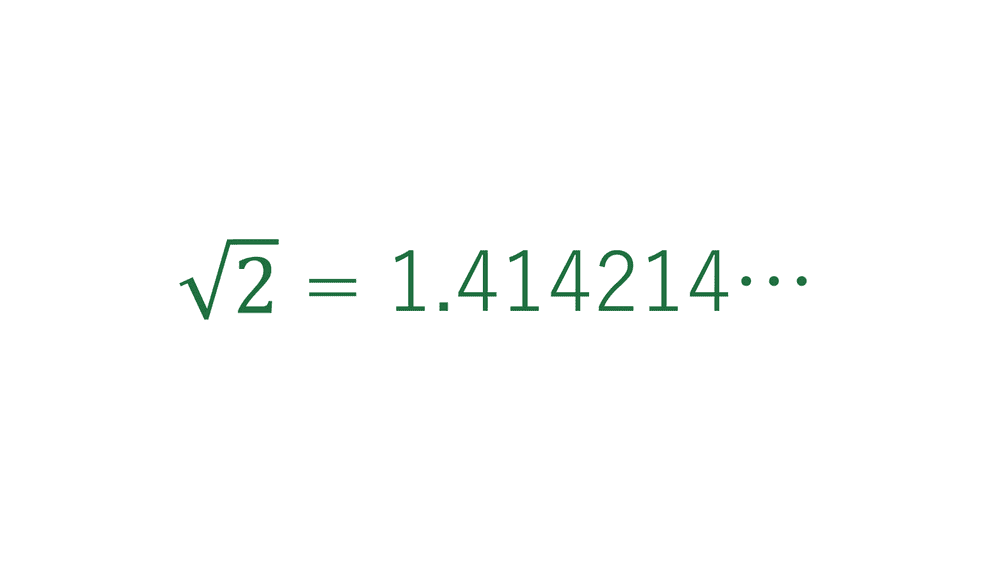 Tossランド 根号を含む式の加減 | 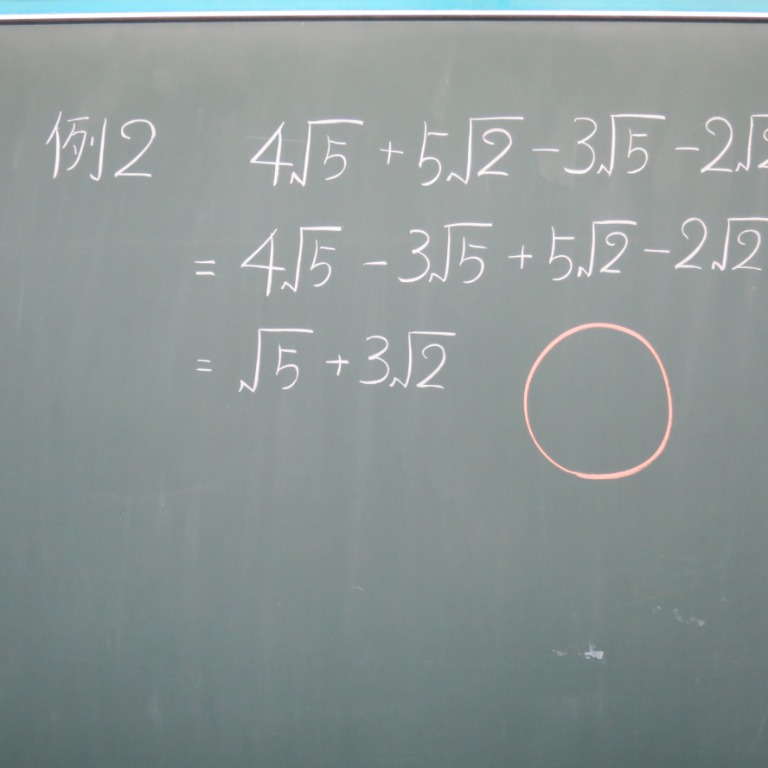 Tossランド 根号を含む式の加減 |
 Tossランド 根号を含む式の加減 |  Tossランド 根号を含む式の加減 | 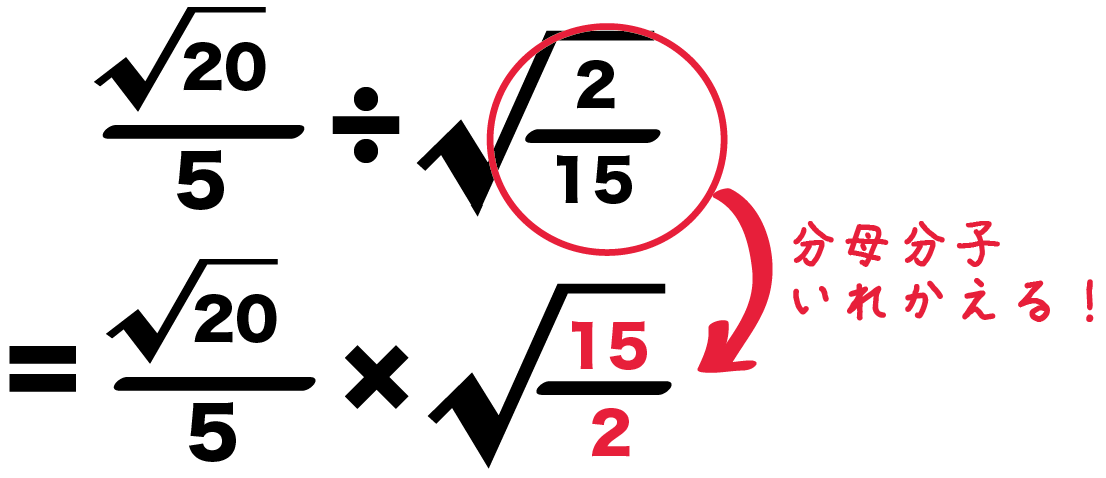 Tossランド 根号を含む式の加減 |
「根号の計算 かけ算」の画像ギャラリー、詳細は各画像をクリックしてください。
 Tossランド 根号を含む式の加減 | Tossランド 根号を含む式の加減 | Tossランド 根号を含む式の加減 |
Tossランド 根号を含む式の加減 |  Tossランド 根号を含む式の加減 |  Tossランド 根号を含む式の加減 |
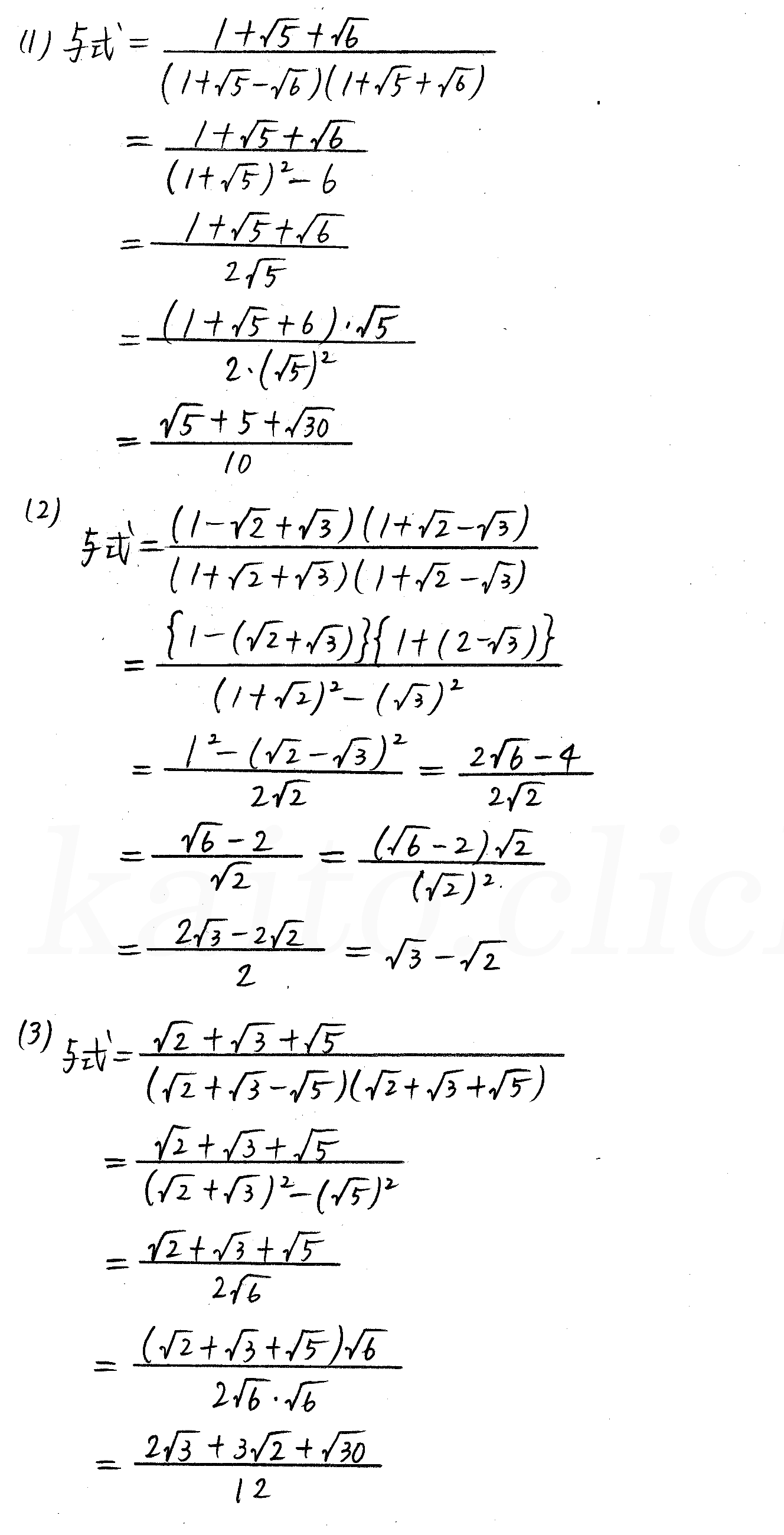 Tossランド 根号を含む式の加減 | Tossランド 根号を含む式の加減 |  Tossランド 根号を含む式の加減 |
「根号の計算 かけ算」の画像ギャラリー、詳細は各画像をクリックしてください。
 Tossランド 根号を含む式の加減 |  Tossランド 根号を含む式の加減 |  Tossランド 根号を含む式の加減 |
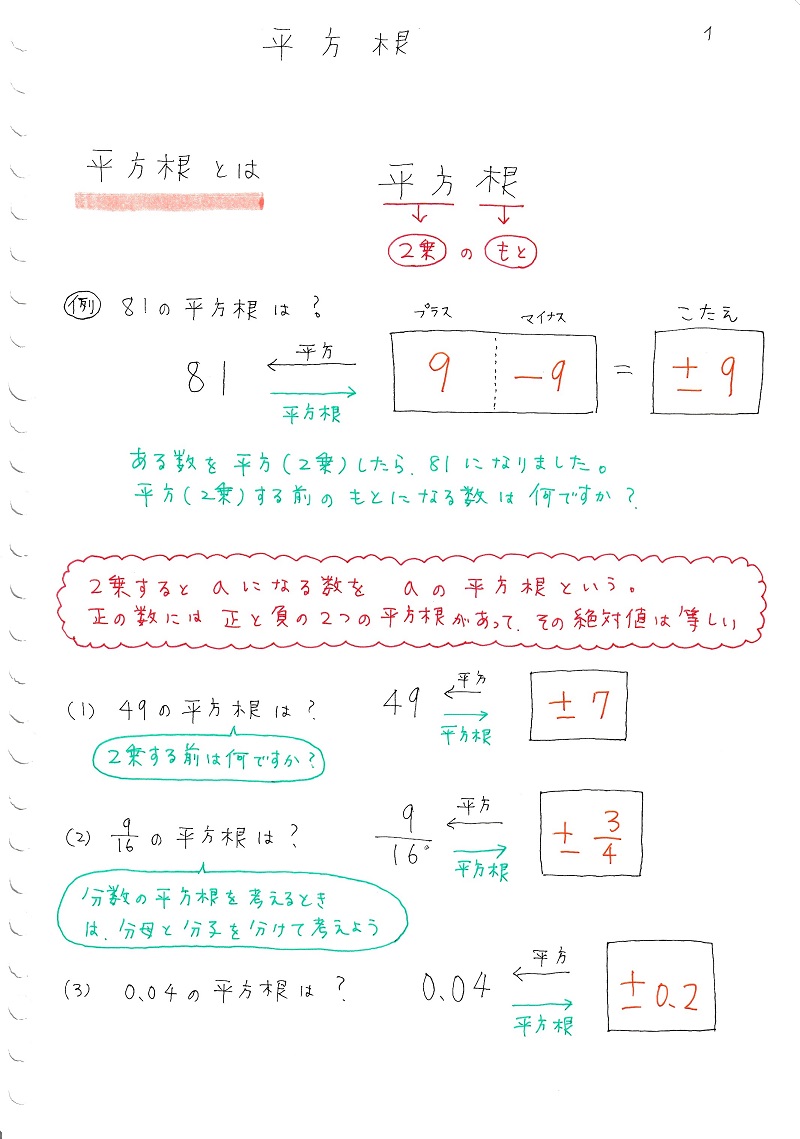 Tossランド 根号を含む式の加減 |  Tossランド 根号を含む式の加減 |  Tossランド 根号を含む式の加減 |
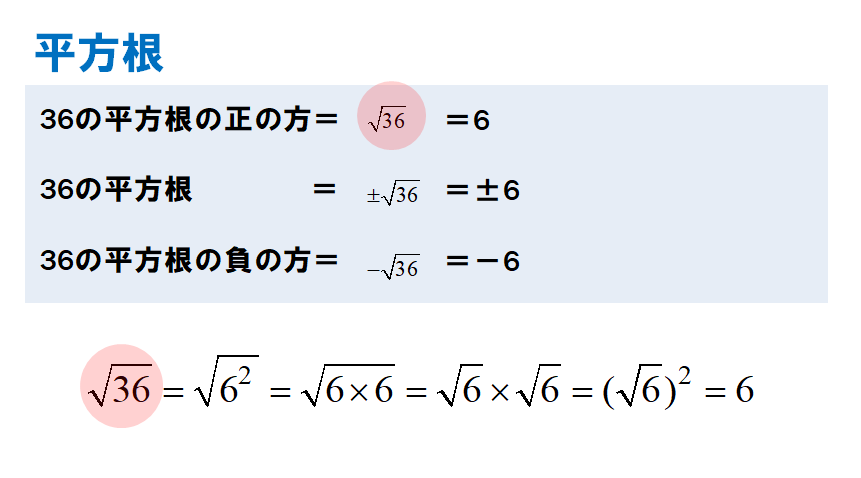 Tossランド 根号を含む式の加減 |  Tossランド 根号を含む式の加減 |  Tossランド 根号を含む式の加減 |
「根号の計算 かけ算」の画像ギャラリー、詳細は各画像をクリックしてください。
 Tossランド 根号を含む式の加減 |  Tossランド 根号を含む式の加減 | Tossランド 根号を含む式の加減 |
 Tossランド 根号を含む式の加減 | Tossランド 根号を含む式の加減 |  Tossランド 根号を含む式の加減 |
 Tossランド 根号を含む式の加減 |  Tossランド 根号を含む式の加減 |  Tossランド 根号を含む式の加減 |
「根号の計算 かけ算」の画像ギャラリー、詳細は各画像をクリックしてください。
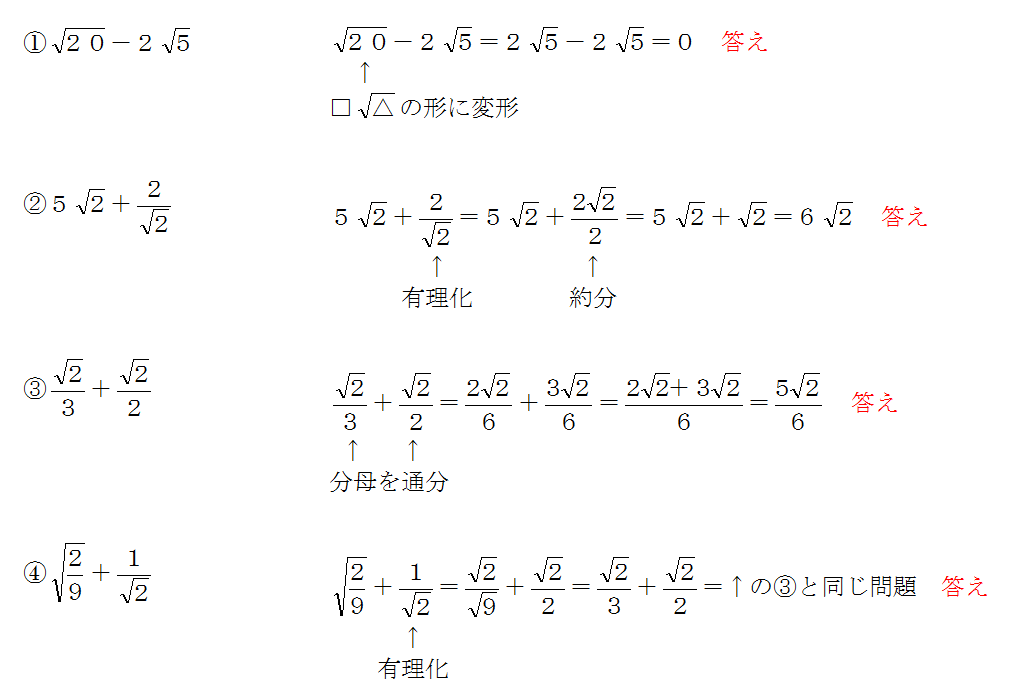 Tossランド 根号を含む式の加減 |  Tossランド 根号を含む式の加減 |  Tossランド 根号を含む式の加減 |
Tossランド 根号を含む式の加減 |  Tossランド 根号を含む式の加減 | 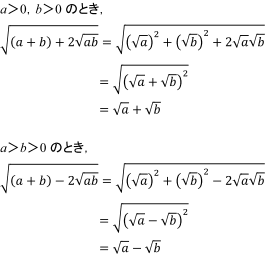 Tossランド 根号を含む式の加減 |
 Tossランド 根号を含む式の加減 |  Tossランド 根号を含む式の加減 |  Tossランド 根号を含む式の加減 |
「根号の計算 かけ算」の画像ギャラリー、詳細は各画像をクリックしてください。
 Tossランド 根号を含む式の加減 |  Tossランド 根号を含む式の加減 |  Tossランド 根号を含む式の加減 |
 Tossランド 根号を含む式の加減 |  Tossランド 根号を含む式の加減 |  Tossランド 根号を含む式の加減 |
 Tossランド 根号を含む式の加減 |  Tossランド 根号を含む式の加減 |  Tossランド 根号を含む式の加減 |
「根号の計算 かけ算」の画像ギャラリー、詳細は各画像をクリックしてください。
 Tossランド 根号を含む式の加減 |  Tossランド 根号を含む式の加減 | Tossランド 根号を含む式の加減 |
 Tossランド 根号を含む式の加減 | Tossランド 根号を含む式の加減 |  Tossランド 根号を含む式の加減 |
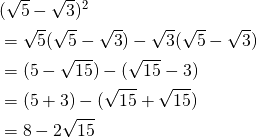 Tossランド 根号を含む式の加減 |  Tossランド 根号を含む式の加減 | Tossランド 根号を含む式の加減 |
「根号の計算 かけ算」の画像ギャラリー、詳細は各画像をクリックしてください。
 Tossランド 根号を含む式の加減 |  Tossランド 根号を含む式の加減 |  Tossランド 根号を含む式の加減 |
 Tossランド 根号を含む式の加減 | 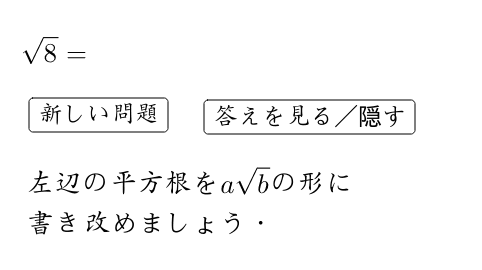 Tossランド 根号を含む式の加減 |  Tossランド 根号を含む式の加減 |
 Tossランド 根号を含む式の加減 |  Tossランド 根号を含む式の加減 |  Tossランド 根号を含む式の加減 |
「根号の計算 かけ算」の画像ギャラリー、詳細は各画像をクリックしてください。
 Tossランド 根号を含む式の加減 |  Tossランド 根号を含む式の加減 | Tossランド 根号を含む式の加減 |
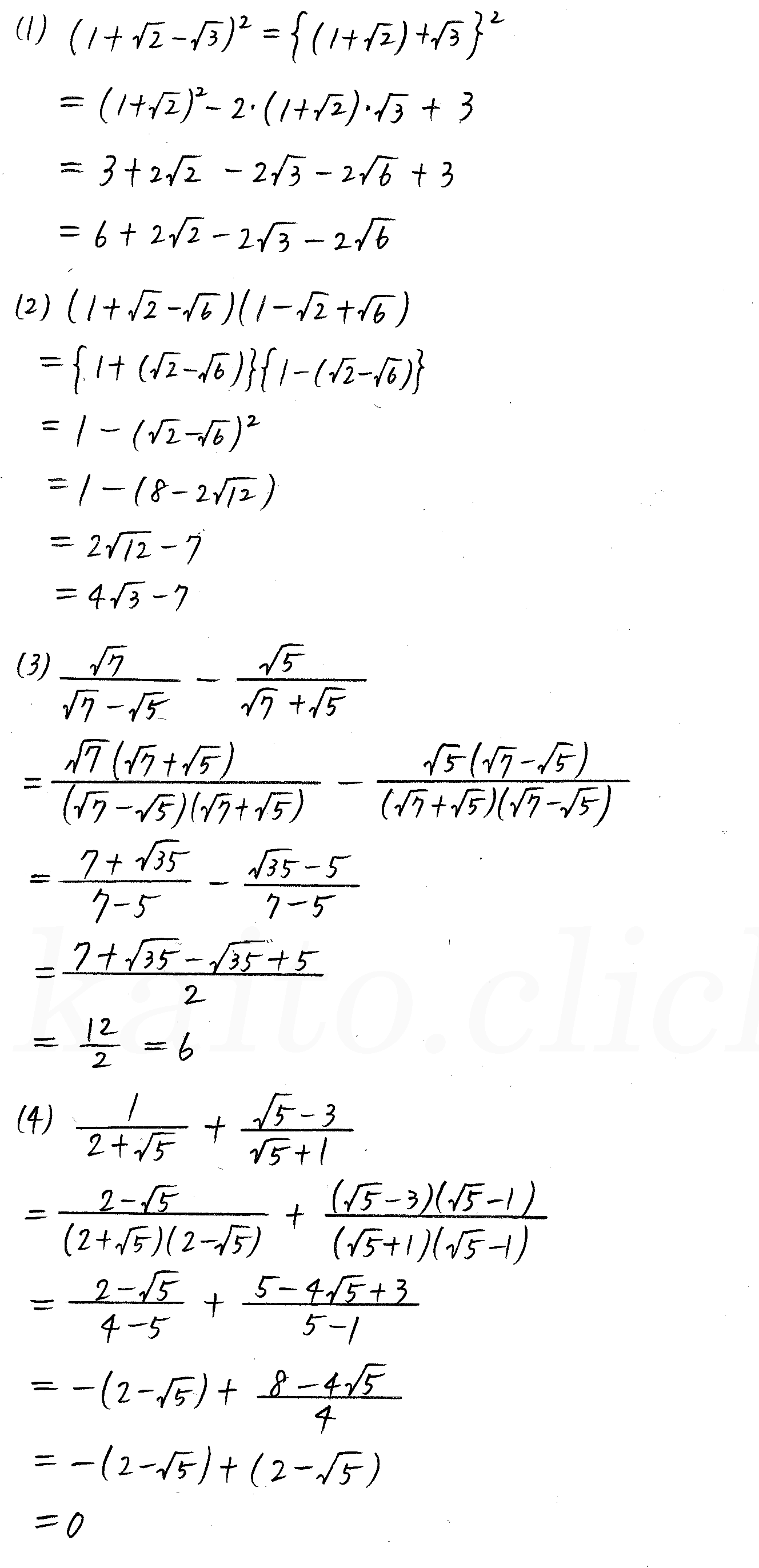 Tossランド 根号を含む式の加減 | Tossランド 根号を含む式の加減 | Tossランド 根号を含む式の加減 |
 Tossランド 根号を含む式の加減 |  Tossランド 根号を含む式の加減 |  Tossランド 根号を含む式の加減 |
「根号の計算 かけ算」の画像ギャラリー、詳細は各画像をクリックしてください。
 Tossランド 根号を含む式の加減 |  Tossランド 根号を含む式の加減 |  Tossランド 根号を含む式の加減 |
 Tossランド 根号を含む式の加減 |  Tossランド 根号を含む式の加減 | Tossランド 根号を含む式の加減 |
 Tossランド 根号を含む式の加減 | 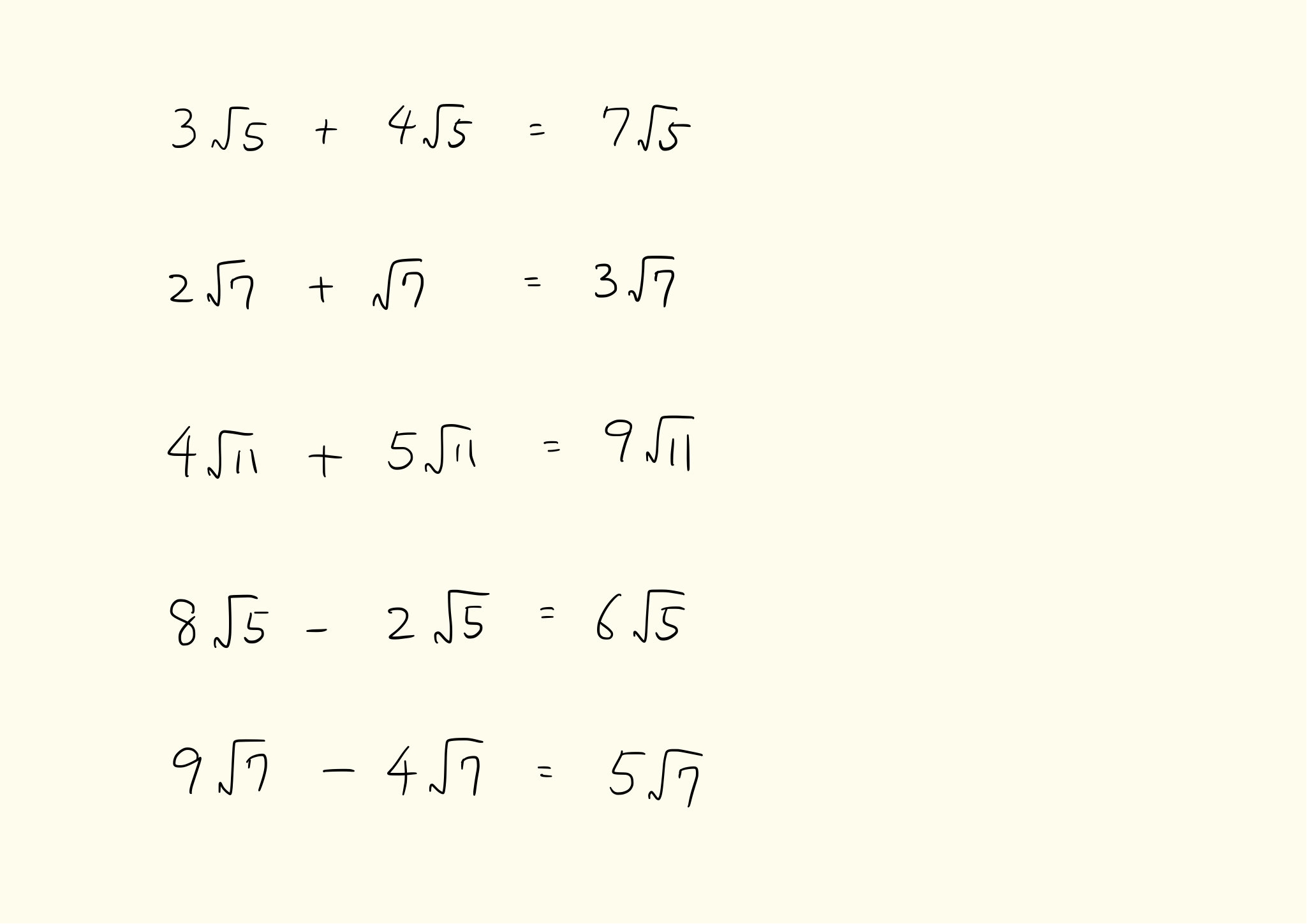 Tossランド 根号を含む式の加減 |  Tossランド 根号を含む式の加減 |
「根号の計算 かけ算」の画像ギャラリー、詳細は各画像をクリックしてください。
 Tossランド 根号を含む式の加減 | 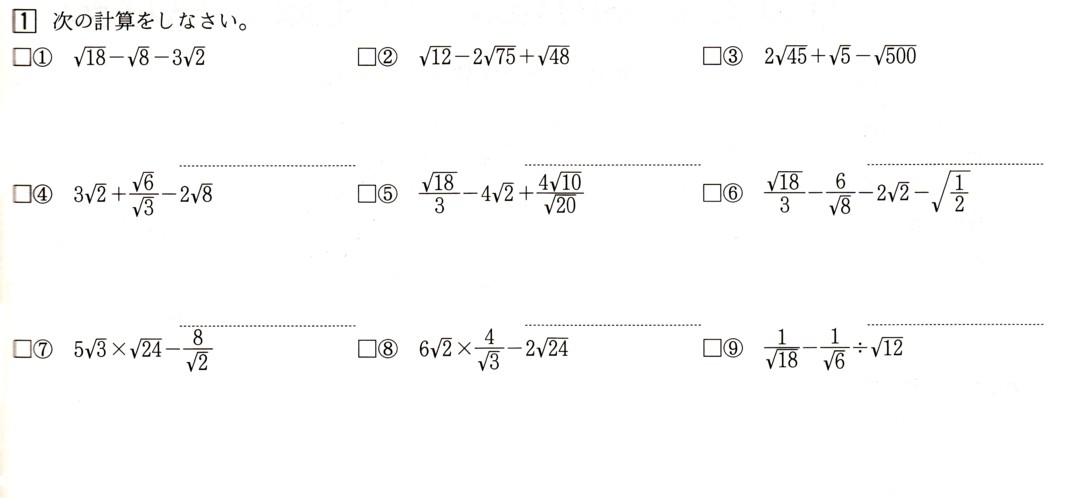 Tossランド 根号を含む式の加減 |  Tossランド 根号を含む式の加減 |
 Tossランド 根号を含む式の加減 |  Tossランド 根号を含む式の加減 |  Tossランド 根号を含む式の加減 |
 Tossランド 根号を含む式の加減 | 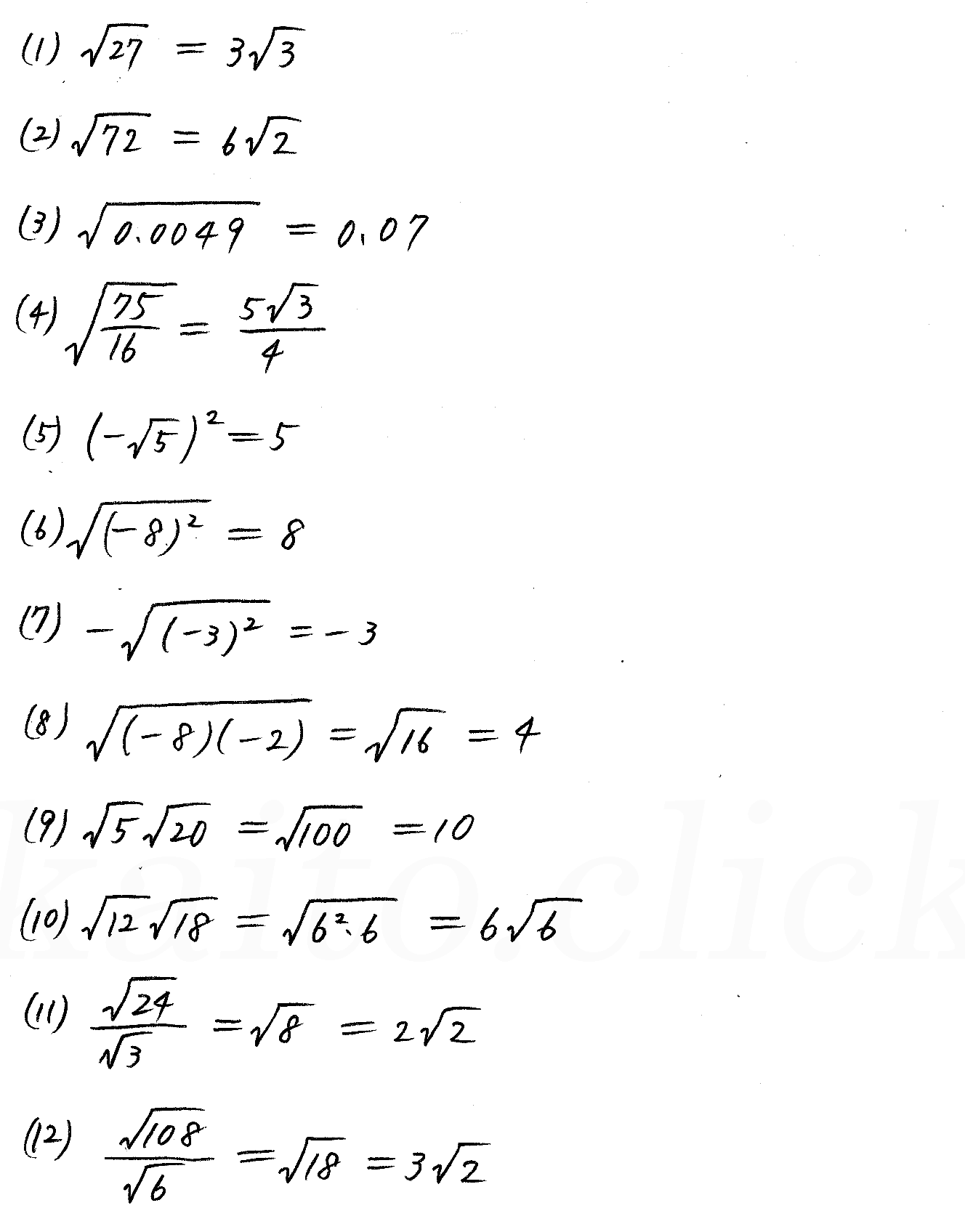 Tossランド 根号を含む式の加減 |  Tossランド 根号を含む式の加減 |
「根号の計算 かけ算」の画像ギャラリー、詳細は各画像をクリックしてください。
 Tossランド 根号を含む式の加減 |  Tossランド 根号を含む式の加減 |  Tossランド 根号を含む式の加減 |
 Tossランド 根号を含む式の加減 | Tossランド 根号を含む式の加減 |
根号の計算の乗法の確認に行く前に,必要な展開公式を復習しておきましょう! 展開の授業で紹介した,展開の公式7選です 詳細は,過去記事を参考にしてください 21年10月23日 数と式①式の展開公式を使って二重根号を外した後に、ルートを簡単にできるパターンがあります。 ルートの中が簡単にできる場合には最後まで気を抜かずに簡単にしておきましょう。 62 5 = (51)2 5×1 = 5 1 = 5 1 <証明> この公式がどうして成り立つかというと、まず
Incoming Term: 根号の計算, 根号の計算 電卓, 根号の計算機, 根号の計算 分数, 根号の計算 かけ算, 根号の計算 問題, 根号の計算 高校,




0 件のコメント:
コメントを投稿